0. 개요
보스턴 주택 가격 데이터셋은 머신 러닝과 회귀 분석 연습용으로 널리 활용되는 데이터셋 중 하나입니다. 이 데이터셋은 미국 매사추세츠주 보스턴 내 다양한 지역의 주택 가격과 주택 가격에 영향을 미치는 여러 가지 특성들을 포함하고 있습니다. 주로 회귀 분석의 예제로 사용되며, 집값을 예측하는 모델을 만들기 위한 데이터로 활용됩니다. 이 데이터셋은 Scikit-learn 라이브러리에 기본으로 내장되어 있어서 불러와서 사용할 수 있는데, 해당 파일을 블로그에도 첨부하였으니 자유롭게 다운하셔도 됩니다. 주요 칼럼값은 아래와 같습니다.
- CRIM: 지역별 1인당 범죄율
- ZN: 25,000 평방피트당 주거용 토지 비율
- INDUS: 비소매상업지역 면적 비율
- CHAS: 찰스 강 인접 여부 (1: 강 인접, 0: 강 미인접)
- NOX: 일산화질소 농도 RM: 주택당 평균 방 개수
- AGE: 1940년 이전에 건축된 주택의 비율
- DIS: 5개의 보스턴 고용 센터와의 거리에 대한 가중치
- RAD: 방사형 고속도로 접근성 지수
- TAX: $10,000당 재산세율
- PTRATIO: 학생-교사 비율
- B: 1000(Bk - 0.63)^2, 여기서 Bk는 지역별 흑인 비율
- LSTAT: 저소득 계층의 비율
- MEDV: 주택 가격의 중앙값
이 데이터셋을 활용하여 다양한 회귀 모델을 학습하고 집값을 예측하는 연습을 할 수 있습니다. 데이터의 다양한 특성을 이해하고 활용하여 모델을 개선하며, 데이터 분석 및 예측 능력을 향상시킬 수 있는 좋은 예제 중 하나입니다.
1. 파이썬 코드 - 회귀분석
#라이브러리 불러오기
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
#데이터 불러오기
boston_data = pd.read_csv('HousingData.csv')
#결측치 확인 및 제거
boston_data.isnull().sum()
boston_data = boston_data.dropna(axis=0)
#데이터 분할
X=boston_data.drop('MEDV',axis=1)
y=boston_data['MEDV']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 선형 회귀 모델 생성 및 학습
model = LinearRegression()
model.fit(X_train, y_train)
#테스트 데이터에 대한 예측
y_pred = model.predict(X_test)
# 평가: 평균 제곱 오차(Mean Squared Error) 계산
mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error: {mse:.2f}')
2. 탐색적 데이터 분석(EDA)
1) 데이터 구조
boston_data.head()
CRIM부터 MEDV까지 총 14개의 칼럼값을 가지고 있습니다.
2) 상관 분석
# 상관 분석 시각화
correlation_matrix = boston_data.corr()
plt.figure(figsize=(12, 8))
sns.heatmap(correlation_matrix, annot=True)
plt.title('Correlation Matrix')
plt.show()
- 'RM' (방 개수)은 'MEDV' (주택 가격)와 양의 상관 관계를 가지는 밝은 색을 보여줍니다. 이는 방의 개수가 증가할수록 주택 가격도 증가하는 경향을 나타냅니다.
- 'LSTAT' (저소득 계층의 비율)은 'MEDV'와 음의 상관 관계를 가집니다. 이는 저소득 계층의 비율이 높을수록 주택 가격이 낮아지는 경향을 나타냅니다.
- 'RAD' (방사형 고속도로 접근성 지수)와 'TAX' ($10,000당 재산세율)는 서로 강한 상관 관계를 보입니다.
3) 주택 가격 분포
# 주택 가격 분포
plt.figure(figsize=(8, 6))
sns.histplot(data=boston_data, x='MEDV', bins=30, kde=True)
plt.title('Distribution of Housing Prices (MEDV)')
plt.show()
4) 방 개수와 주택 가격간 관계
# 방 개수와 주택 가격 분포
plt.figure(figsize=(8, 6))
sns.scatterplot(data=boston_data, x='RM', y='MEDV')
plt.title('Relationship between Rooms (RM) and Housing Prices (MEDV)')
plt.show()
3. 결측값 확인
파이썬에서 결측값을 확인하고 처리하는 방법은 데이터 전처리 과정에서 중요한 부분입니다.
boston_data.isnull().sum()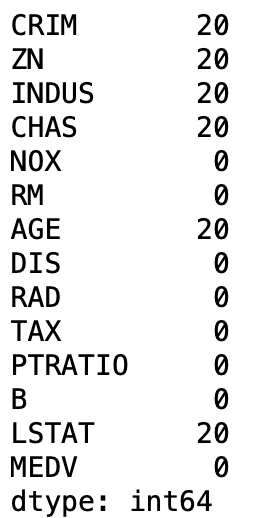
결측값을 지우는 방법도 있고, 평균이나 최빈값으로 대체하는 방법도 있는데 나는 지우는 방법을 선택하였습니다.
boston_data = boston_data.dropna(axis=0)
4. 모델 성능 평가
1) 성능 평가
# 평가: 평균 제곱 오차(Mean Squared Error) 계산
mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error: {mse:.2f}')Mean Squared Error: 31.45
파이썬 머신러닝에서 모델 성능 평가는 매우 중요한 이유가 있습니다. 모델의 성능을 평가하는 것은 모델이 얼마나 좋은 예측을 하는지를 이해하고 개선하는 데 도움을 주는 핵심적인 단계입니다.
- 비즈니스 의사 결정에 활용: 머신러닝 모델은 비즈니스 의사 결정을 지원하는 데 사용될 수 있습니다. 모델의 예측 능력이나 신뢰도를 평가함으로써, 예를 들어 상품 판매 예측, 금융 리스크 평가 등과 같은 중요한 결정에 도움을 줄 수 있습니다.
- 성능 개선: 성능 평가를 통해 모델의 약점이나 부족한 부분을 파악하고 개선할 수 있습니다. 예측의 정확도를 높이거나 편향을 줄이는 등 모델을 보다 강력하게 만들기 위한 방법을 찾을 수 있습니다.
- 과적합 및 과소적합 판단: 모델 성능 평가는 과적합(Overfitting)이나 과소적합(Underfitting)과 같은 문제를 판단하는데 도움을 줍니다. 훈련 데이터에 대한 예측 능력과 테스트 데이터에 대한 예측 능력을 비교하여 모델의 일반화 능력을 평가할 수 있습니다.
- 모델 해석: 모델의 성능 평가 결과는 모델이 어떤 특성을 중요하게 생각하는지, 어떤 특성이 예측에 큰 영향을 주는지 등을 파악하는 데 도움을 줍니다.
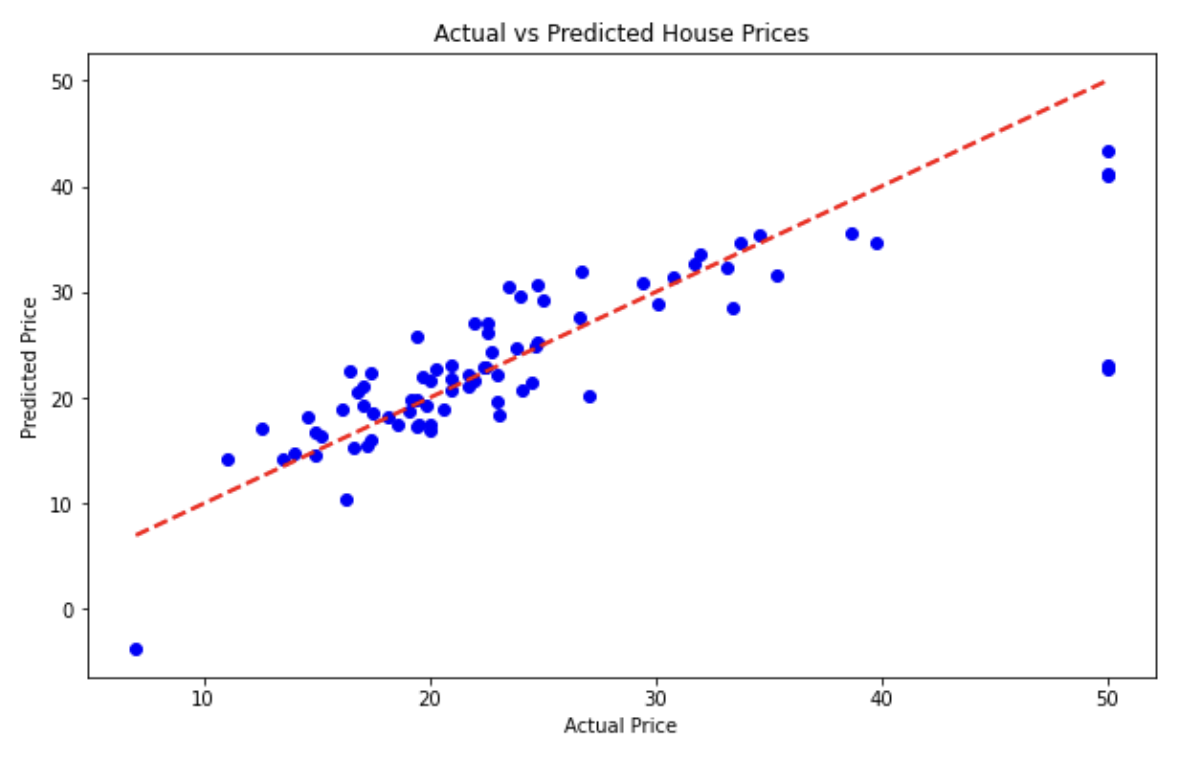
2) 시각화 - 실제값과 예측값을 비교하는 그래프
#라이브러리
import matplotlib.pyplot as plt
#그래프 설정
plt.figure(figsize=(10, 6))
plt.scatter(y_test, y_pred, color='blue')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], linestyle='--', color='red', linewidth=2)
plt.xlabel('Actual Price')
plt.ylabel('Predicted Price')
plt.title('Actual vs Predicted House Prices')
plt.show()
'Python, R 분석과 프로그래밍 > 머신러닝' 카테고리의 다른 글
| [Python] 로지스틱 회귀분석(logistic regression) - breast_cancer (1) | 2024.01.14 |
|---|---|
| 머신 러닝 - 타이타닉 생존자 분석 (0) | 2023.08.13 |